Utility Maximization
Utility Maximization Assignment Help | Utility Maximization Homework Help
Utility Maximization: Optimal Consumer Choice
We have described two of the three parts we need to explain how consumers choose goods. First, we described their limitations (scarceness; income; the budget line), and then we described their preferences (desires, taste). Now, we put these two parts together. Moreover, if we add the assumption that the consumer will maximize her utility, we will be able to predict which basket of goods she will choose: She will choose a point on an indifference curve that she can afford and that gives her maximum utility. This usually, but not always, singles out one point.
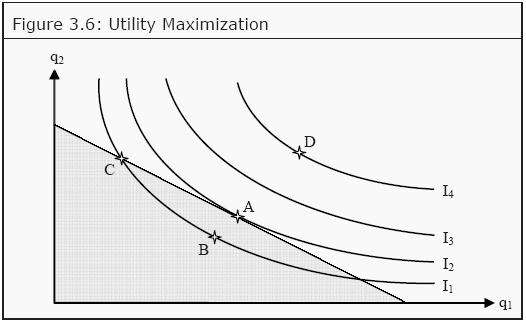
In Figure 3.6, we see the indifference curves from Figure 3.4 and the budget line from Figure 3.1 combined. Which of the points A – D is an optimal, utility maximizing, choice?
1- Is, for instance, point B optimal? No, A is better than B since A is on a higher indifference curve. The consumer can also afford A, since A is on the budget line.
2- Is C optimal? No, C is on the same indifference curve as B, and is therefore as good as B. However, A is better than B and, consequently, A must be better than C.
3- Is D optimal? D is on a higher indifference curve than any of the other baskets, A – C. It therefore produces the highest level of utility. However, the consumer cannot afford D since it lies outside the budget line. Therefore, D is not an optimal choice.
4- Is A optimal? Yes, A is the only basket that, given the consumers indifference curves and budget line, produces a maximum level of utility. All other points that lie on or below the budget line produce lower levels of utility. At point A, an indifference curve just touches the budget line (i.e. the budget line is a tangent to the indifference curve). Point A has an interesting property. In that point, the budget line and the indifference curve have exactly the same slope. Remember that the slope of the budget line is (minus) the quotient between the prices -p2/p1, which we called the marginal rate of transformation (MRT), and that the slope of the indifference curves is the marginal rate of substitution (MRS). A criterion for being exactly at the point where we maximize utility is then that
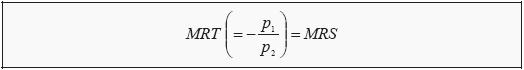
However, there are cases when the point of utility maximization does not fulfill this criterion. Look for instance at the indifference curves for perfect substitutes and complementary goods. If you fit a budget line into any of those graphs, you will find that the criterion
marginal rate of transformation (MRT) = marginal rate of substitution (MRS) usually is not fulfilled. For perfect substitutes, the consumer will usually maximize her utility at either the X-axis or at the Y-axis, where she only consumes one of the goods (this is called a corner solution; the opposite is called an interior solution). If the budget line is parallel to an indifference curve, the consumer can choose any point on the line. She can afford them all, and she is indifferent between all of them.
For complementary goods, she will maximize her utility at a point where an indifference curve has a corner. In such a point, the curve has no defined slope (since it has different slopes to the left and to the right) and, hence, MRS does not exist.
Use the following strategy to find the point of utility maximization:
1- Draw the budget line.
2- Find the indifference curve that just barely touches the budget line (i.e. an indifference curve that the budget line is a tangent to). In most cases, there is only one such indifference curve. All other indifference curves either crosses the budget line or does not touch it at all. Be careful, however, to check if there exists a corner solution.
3- The point of utility maximization is the point of tangency (or the corner solution).

In Figure 3.6, we see the indifference curves from Figure 3.4 and the budget line from Figure 3.1 combined. Which of the points A – D is an optimal, utility maximizing, choice?
1- Is, for instance, point B optimal? No, A is better than B since A is on a higher indifference curve. The consumer can also afford A, since A is on the budget line.
2- Is C optimal? No, C is on the same indifference curve as B, and is therefore as good as B. However, A is better than B and, consequently, A must be better than C.
3- Is D optimal? D is on a higher indifference curve than any of the other baskets, A – C. It therefore produces the highest level of utility. However, the consumer cannot afford D since it lies outside the budget line. Therefore, D is not an optimal choice.
4- Is A optimal? Yes, A is the only basket that, given the consumers indifference curves and budget line, produces a maximum level of utility. All other points that lie on or below the budget line produce lower levels of utility. At point A, an indifference curve just touches the budget line (i.e. the budget line is a tangent to the indifference curve). Point A has an interesting property. In that point, the budget line and the indifference curve have exactly the same slope. Remember that the slope of the budget line is (minus) the quotient between the prices -p2/p1, which we called the marginal rate of transformation (MRT), and that the slope of the indifference curves is the marginal rate of substitution (MRS). A criterion for being exactly at the point where we maximize utility is then that
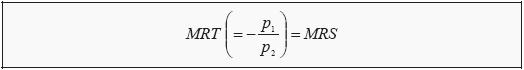
However, there are cases when the point of utility maximization does not fulfill this criterion. Look for instance at the indifference curves for perfect substitutes and complementary goods. If you fit a budget line into any of those graphs, you will find that the criterion
marginal rate of transformation (MRT) = marginal rate of substitution (MRS) usually is not fulfilled. For perfect substitutes, the consumer will usually maximize her utility at either the X-axis or at the Y-axis, where she only consumes one of the goods (this is called a corner solution; the opposite is called an interior solution). If the budget line is parallel to an indifference curve, the consumer can choose any point on the line. She can afford them all, and she is indifferent between all of them.
For complementary goods, she will maximize her utility at a point where an indifference curve has a corner. In such a point, the curve has no defined slope (since it has different slopes to the left and to the right) and, hence, MRS does not exist.
Use the following strategy to find the point of utility maximization:
1- Draw the budget line.
2- Find the indifference curve that just barely touches the budget line (i.e. an indifference curve that the budget line is a tangent to). In most cases, there is only one such indifference curve. All other indifference curves either crosses the budget line or does not touch it at all. Be careful, however, to check if there exists a corner solution.
3- The point of utility maximization is the point of tangency (or the corner solution).