Normalized and Orthogonal wave functions

As stated in Sec.dT is proportional to the probability of finding the particular system in the small volume element dT. For most of the purposes, it is taken as equal to rather than proportional to the probability. In such a case, the integration of dt  over the whole of the configuration space , which gives the total probability, must be equal to unity i.e.,

                                         
Whererepresents the integration over the whole space.

A wave function which satisfies the above equation is said to be normalized.

In most of the cases, the result of integration is found to be equal to some constant, say N. Then we have
                                             

To make the result equal to unity, we have
                                               
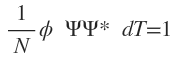
 or                                                         

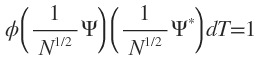
The factor thus introduced is called the normalization constant and the function is called the normalized function. It is found that the normalized function is also a solution of the wave equation just like the anomalies wave function.

If and are two different eigen functions obtained as satisfactory solutions of the wave equation hen as stated above ,these functions will be normalized if
                   

Further if they satisfy the following conditions
                      

They are said to be mutually orthogonal.
Wave functions that are solutions of a given Schrodinger equation are usually orthogonal to one another.
Wave-functions that are both orthogonal and normalized are called or tonsorial.

For more help in Normalized and Orthogonal wave functions click the button below to submit your homework assignment