Ampere’s law in Curl Form or Curl B and Stokes’ Theorem

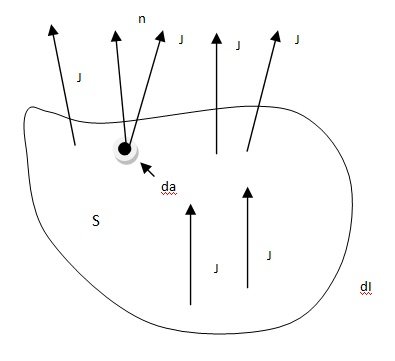
Consider a region in which there is steady flow of charge. The current density J in this region remains constant, i.e., the current density J does not change with time. However its value may vary from place to place.

The total current enclosed by the path
            I = ∫_x J. da                                … (1)
 Here, d a = n da is small element of area at the point of current density J inside the closed path. n is unit vector normal to elementary area da. Now from Ampere’s law in circuital form, the line integral of the magnetic induction B around the closed path is
       
    Ï• = B. dl = μ₀ x current enclosed by the path = μ₀ I
        = μ₀ ∫s J . da                                    … (2)

But from Stoke’s theorem
        Φ B.dl = ∫_x  curl B . da                                … (3)

Comparing Eqs. (2) and (3), we get
        ∫_x  curl B . da = μ0  ∫s J. da
or    ∫_x  (curl B – μ₀ J) . da = 0
As the surface is arbitrary, we have
    Curl B - μ₀ J = 0
        Curl B = μ₀ J 

For more help in Ampere’s law in Curl Form or Curl B and Stokes’ Theorem please click the button below to submit your homework assignment