Application Of Maxwells Cycle
Application Of Maxwells Cycle Assignment Help | Application Of Maxwells Cycle Homework Help
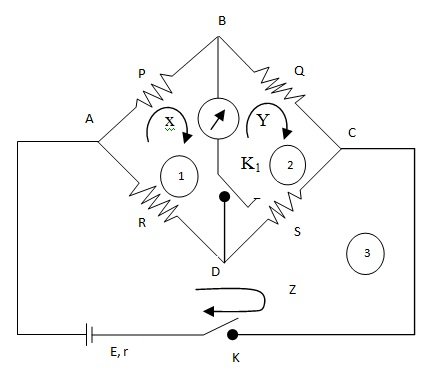
Application of Maxwell’s Cycle Current Method to Whetstone’s bridge
According to this method, a cyclic current of some specific value is imagined to flow in each mesh and all the currents in various meshes are assumed to flow in the same direction i.e., clockwise or anticlockwise. The actual current flowing in any branch of the mesh is the algebraic sum of the cyclic currents flowing in the meshes which the branch separates. Further, the e.m.f is taken as positive if it sends the current in the same direction in which the cycle current is assumed to flow and negative If it sends the current in the opposite direction.Let x, y and z be the currents flows in the clockwise direction through the meshes (1) ABDA, (2) BCDB, and (3) ADCEA.
Applying Kirchhoff’s second law to the meshes (1), (2) and (3),
xP + (x – y)G + (x – z)R = 0 … (1)
yQ + (y – z) S + (y – x)G = 0 … (2)
and (z – x)R + (z – y)s + zr = E … (3)
Collecting the coefficient of x, y and z in Eqs. (1) and (2),
x (P + G + R) – yG – zR = 0 … (4)
and -xG + y (Q + S + G) – zS = 0 … (5)
Multiplying Eq. (4) by S and Eq. (5) by R and subtracting, we get,
x [S(P + G + R) + RG] – y[GS + R (Q + S + G)] = 0
The current passing through the galvanometer = (x – y). When the bridge is balanced, the current through the galvanometer is zero,
i.e., x – y = 0 or x = y
. : SP + SG + SR + RG = GS + RQ + RS + RG
Or SP = RQ or P/Q = R/S … (6)
Eq. (6) is the necessary condition for a balanced Wheatstone bridge.
For more help in Application of Maxwell’s Cycle Current Method to Whetstone’s bridge click the button below to submit your homework assignment