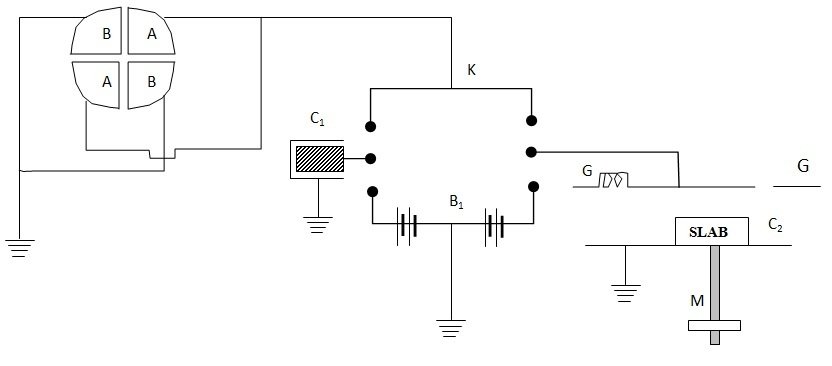
Dielectric Constant of a Solid – Hopkinson’s Null Method

This method is applicable to solids available in the form of a slab. The needle of quadrant electrometer is given a constant potential V using a battery. C₁ is a variable capacitor. C₂ is a guard ring capacitor in which the lower earthed plate is movable. The distance through which the lower plate of C₂ is moved can be measured using a micrometer screw M. The mid-point of the battery B₁ is earthed so using a micrometer screw M. The mid-point of the battery B₁ is earthed so that its end points are kept at potential difference +V and –V with respect to the earth. Using this arrangement the capacitors C1 and C₂ can be charged to equal and opposite potentials by pressing the key K. On releasing the key, the capacitors charge the quadrant electrometer. If their capacitances are also made equal by suitably varying C₁, their charges will become equal and the electrometer will show zero deflection. So the method is called a null method.

Working. The capacitance of the variable capacitor C₁ is adjusted till on pressing and releasing the key, there is no deflection in the quadrant electrometer. Now the position of the lower plate of C₂ is read on the micrometer scale. The dielectric slab of thickness t and dielectric constant (relatives permittivity) εr is introduced between the plates of C₂. As a result the capacitance of C₂ increases. The lower plate of C₂ is moved till the electrometer shows null deflection. Now the capacitance of C₂ is moved till the electrometer shows null deflection. Now the capacitance of C₂ is equal to that of C₁.  The distance x through which the lower plate of C₂ has been moved is measured using the micrometer screw. Let A be the effective area of guarding capacitor plates and d the distance between them.

Then, capacitance of C₂ without the dielectric = ε₀A/d

Capacitance of C₂ with the dielectric = ε₀A/ (d + x – t + t/ε_r)

But the capacitance in the two cases in the same.

Hence , ε₀A/d = ε₀A/ (d + x – t + t/ε_r)

i.e.,     d = d + x – t + t/ ε_r

. :    ε_r = t/(t – x)

For more help in Dielectric Constant of a Solid – Hopkinson’s Null Method please click the button below to submit your homework assignment.