Dielectric Sphere in a Uniform Field

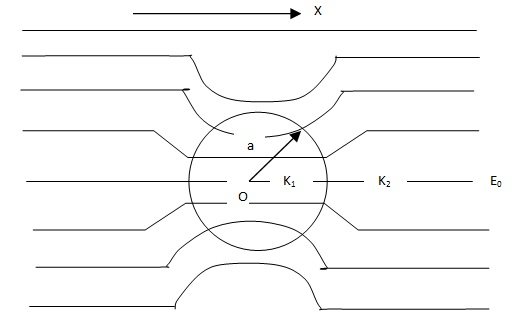
Consider an uncharged dielectric sphere of radius a and dielectric constant K₁, surrounded by a medium of dielectric constant K₂ and placed in a uniform electric field E0. The origin of the coordinate system is taken to be at the centre of the sphere and the X axis along E0. Let V₁ and V₂ be the potential function inside and potential functions inside and outside the sphere respectively. The solution to this problem must satisfy the following boundary conditions.
(i)    ∇²V₁ = 0 and ∇²V₂ = 0, both inside and outside respectively, as the net charge on the sphere is zero.
(ii)    V₁ must remain finite for all r < a. V₂ must also remain finite at infinity.
(iii)    V₁ = V₂ for r = a at all angles θ.
(iv)    The normal component of D must be continuous at r = a, i.e., D_1n = D_2n.

The potentials outside and inside the sphere can be written as:
        V₂ = - E₀ r cos θ + (A/r²) cos θ                            … (1)
        V₁ = Br cos θ + (C/r²) cos θ                            … (2)

C must be zero. Otherwise, the potential would become infinite at the origin (r = 0). Hence
        V₁ = B_r cos θ                                    … (3)

According to the boundary condition (iii), V₁ = V₂, for r = a
    . :     Ba cos θ = -E₀a cosθ + (A/a²) cos θ or B = -E₀ + a/a³                … (4)

According to the boundary condition (iv),
        D_1n = D_2n or K₁ε₀ E_1n = K₂ε₀ E_2n
Now,         E_n = -∂V/∂r
Hence,         - K₁ (∂V₁/∂r) r = a = -K₂ (∂V₂/∂r)_{r = a}
        - K₁B cos = -K₂ [-E₀ cosθ – (2A/a³) cos θ]
Or        K₁bB = -K₂ (E₀ + 2A/a³)                                … (5)
    Solving Eqns. (4) and (5), we get
        A = (K₁ – K₂/K₁ + 2K₂) E₀a³    and B = (-3K₂/K1 + 2K₂)E₀

Thus the potential function inside and outside the spheres are:
    V₁ = - (3K₂/K₁ + 2K₂) E₀ r cos θ                                … (6)
    V₂ = - [1 – (K₁ – K₂/K₁ + 2K₂) a³/r³] E₀ r cos θ                        … (7)

The electric field at any point inside the sphere is
    E₁ = - ∂V₁/∂x = (3K₂/K₁ + 2K₂) E0 [. : = - (3K₂/K₁ + 2K₂)E₀x]                … (8)

The potential outside the sphere is equivalent to the applies field E0 plus the field of an electric dipole at centre of sphere with dipole moment.
        p = 4πε₀K₂ (K₁ – K₂/K₁ + 2K₂) E₀a³                        … (9)
oriented in the direction of applied field.

We know that when a dielectric sphere acquires a dipole moment in the field, it is polarized. The polarization is defined as the dipole moment per unit volume i.e.,
        Polarization = P/(4/3)πa³ = 3ε₀ K₂ (K₁ – K₂/K₁ + 2K₂) E₀                … (10)



For more help in Dielectric Sphere in a Uniform Field please click the button below to submit your homework assignment.