Electrostatic Boundary Conditions

Let us examine how the electric field changes at the boundary between two different media. Let us fine amount by which E changes at such a boundary.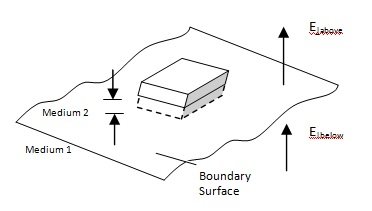


(A)    Let us construct a small Gaussian pillbox, extending just barely over the edge in each direction. A is the area of the pillbox lid, h is the thickness of the pillbox. Applying Gauss’s law,
Φ E. da = 1/ε₀ Q_enc = 1/ε₀ σA,

Now, the sides of the pillbox contribute nothing to the flux as h  O. So
E| _above – E| _below = 1/ε₀ σ                                    … (1)

Here, E|_above denotes the component of E that is perpendicular to the surface immediately above, and E|_above denotes the component of E that is perpendicular to the surface immediately above, and E|_below is the same, only just below the surface. For consistency we let “upward” be the positive direction for both.

According to Eq. (1), the normal component of E is discontinuous by an amount σ/ε₀ at any boundary.
If the boundary is free from charge, σ = 0, then E| is continuous, i.e., the normal component of E is continuous across a charge free boundary.

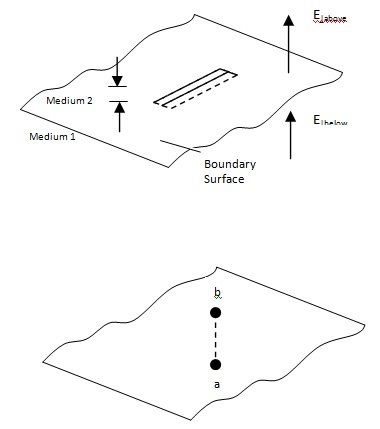
(B) Since the electrostatic field is conservative,
Φ E. dl = 0
around the rectangular path EFGH. The lengths EF and GH will be taken equal to 1 and the segments FG and HE will be assumed to be negligibly small (h 0).  Therefore


or        E_||above l – E_||below l) = 0
            E|_|above = E_||below         … (2)

Here, E_|| represents the components of E which is parallel to the surface. Thus the tangential electric field is continuous across such a boundary. The boundary conditions on E [Eqs. (1) and (2)] can be combined into a single formula:
        E_above – E_below = σ/ε₀ n,                                … (3)
Here, n is a unit vector perpendicular to the surface.

(C)    The electrostatic potential must be continuous across any boundary, since
V_above - V_below = - ∫^b_a E.dl
As the path length shrinks to zero, so too does the integral.
. :    V_above = V_below                                         … (4)
From Eq. (3),
    ∇V_above - ∇V_below = - 1/ε₀ σn                    (. : E = - ∇V)
Or,    ∂ V_above /∂n - ∂ V_below /∂n = - 1/ε₀ σ                                … (5)
Here,     ∂V /∂n = ∇V. n denotes the normal derivative of V.





For more help in Electrostatic Boundary Conditions please click the button below to submit your homework assignment