Inductance And Resistance In Series
Inductance And Resistance In Series Assignment Help | Inductance And Resistance In Series Homework Help
AC Circuit Containing Inductance and Resistance in Series
Let an alternating emf E = E0ejωt be applied to a circuit having an inductance L and a non-inductive resistance R in series.
The potential drop across the inductance is
VL = jωL I
The potential drop across resistance is
VR = RI
Here, I is the current at any instant t.
. : E = jωL I + RI
Current in the circuit,
I = E/R + jωL … (1)
But I = E/Z … (2)
Impedance of R-L circuit,
Z = R + jωL … (3)
. : I = E0 ejωt/√(R2 + ω2L2) ejθ (where tan θ = ωL/R)
= E0 /√R2 + ω2L2) ej(ωt – 0) … (4)
= I0 ej(ωt-θ) … (5)
Here, I0 = E0 /√R2 + ω2L2) … (6)
It represents the peak value of the current through the circuit.
The impedance Z of the circuit is given by the term
√(R2 + ω2L2).
The current lags in phase behind the emf by an angle θ = tan-1 ωL/R.
The variation of instantaneous values of emf and current with time are represented graphically.
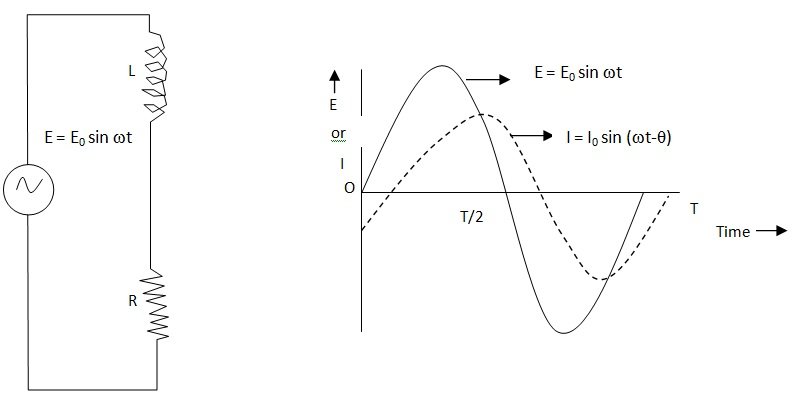
For more help in AC Circuit Containing Inductance and Resistance in Series please click the button below to submit your homework assignment.
The potential drop across the inductance is
VL = jωL I
The potential drop across resistance is
VR = RI
Here, I is the current at any instant t.
. : E = jωL I + RI
Current in the circuit,
I = E/R + jωL … (1)
But I = E/Z … (2)
Impedance of R-L circuit,
Z = R + jωL … (3)
. : I = E0 ejωt/√(R2 + ω2L2) ejθ (where tan θ = ωL/R)
= E0 /√R2 + ω2L2) ej(ωt – 0) … (4)
= I0 ej(ωt-θ) … (5)
Here, I0 = E0 /√R2 + ω2L2) … (6)
It represents the peak value of the current through the circuit.
The impedance Z of the circuit is given by the term
√(R2 + ω2L2).
The current lags in phase behind the emf by an angle θ = tan-1 ωL/R.
The variation of instantaneous values of emf and current with time are represented graphically.

For more help in AC Circuit Containing Inductance and Resistance in Series please click the button below to submit your homework assignment.