Inductance in Parallel

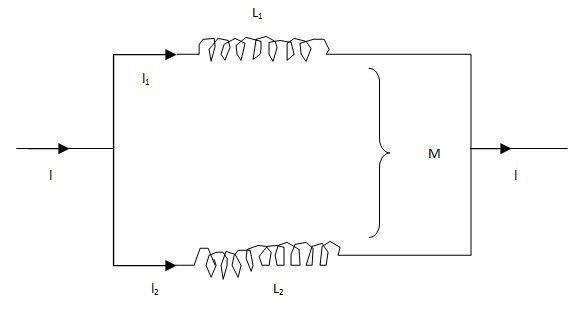
Two inductors L₁ and L₂ are connected in parallel. Let M be their mutual inductance. Let I be the main supply current and I₁ and I₂ the branch currents. Consider a case when self-induced e.m.f. and mutually induced e.m.f. are in same direction.

The e.m.f. in coil I (L₁) is
        ε₁ = L₁ dI₁/dt + M dI₂/dt                                … (1)

The e.m.f. in coil 2 (L₂) is
        ε₂ = L₂ dI₂/dt + M dI₁/dt                                … (2)

In parallel arrangement, ε₁ = ε₂ = ε
    . :    L₁ dI₁/dt + MdI₂/dt = L₂ dI₂/dt + M dI₁/dt
        (L₁ – M)dI1/dt = (L₂ – M)dI2/dt
    . :     dI₁/dt = (L₂ – M/ L₁ – M) dI₂/dt

Substituting this is Eq. (2),
        ε = L₂ dI₂/dt + M (L₂ – M/ L₁ – M) dI₂dt
= [L₂ + M (L₂ – M /L₁ – M)] dI₂/dt
. : ε (L₁ – M) = (L₁L₂ – M₂) dI₂/dt                                    … (3)

Similarly, eliminating dI2/dt from Eq. (2),
    ε (L₂ – M) = (L₁L₂ – M₂)dI1/dt                                … (4)

Adding Eqs. (3) and (4),
    ε (L₁ + L₂ – 2M) = (L1L2 – M2) (dI1/dt + dI2/dt)
But I = I₁ + I₂
    dI/dt = dI₁/dt + dI₂/dt
. :    ε = (L₁L₂ – M₂/ L₁ + L₂ – 2M) dI/dt                            … (5)

If L is equivalent inductance, then ε = LdI/dt                                … (6)

. :        L = L₁L₂ – M₂ /L₁ + L₂ – 2M                            … (7)

If the inductors are connected in such a way that the flux due to self induction opposes the flux due to mutual induction, then
        L = L₁L₂ – M2 /L₁ + L₂ + 2M                            … (8)

For more help in Inductances in Parallel please click the button below to submit your homework assignment.