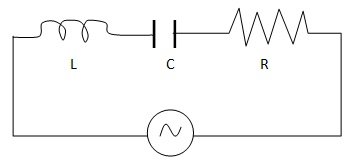
LCR Circuit (Series Resonance Circuit)

Consider a circuit containing an inductance L, a capacitance C and a resistance R joined in series. This series circuit is connected to an AC supply given by

    E = E₀ e^jωx                                     … (1)
The total complex impedance is
Z = Z_R + Z_L + Z_C
= R + j [ω_L – 1/ωC]
= √R₂ + (ω_L – 1/ωC)² e^jφ                                 … (2)
= where tan φ = (ωL – 1/ωC)/R

Using Ohm’s law in complex from, the ‘complex’ current in the circuit is

   
I=E/Z=(E₀ e^jωt)/√(R²+(ωL-1/ωC)² e^jΦ )

I=E₀/√(R²+(ωL-1/ωC)² ) e^{j(ωt- Φ) _}______________________  … (3)


But  I₀=E/Z=E₀/√(R²+(ωL-1/ωC)² )

. : I = I0 ej(ωt – Φ)                                         … (4)

The actual emf is the imaginary part of the equivalent complex emf. Hence the actual current in the circuit is obtained by taking the imaginary part of the above ‘complex’ current.

    . :    i = Im. (I) = E₀/√(R₂+(ωL-1/ωC)²) sin(ωt- Φ)                    … (5)

The equivalent impedance of the series LCR circuit is
   
        √(R²+(ωL-1/ωC)²  )

The current ‘lags’ behind the voltage by an angle
Φ = tan^-1 (ωL-1/ωC)/R



For more help in LCR Circuit (Series Resonance Circuit) click the button below to submit your homework assignment.