Magnetic Field for a Long Straight Current Carrying Wire

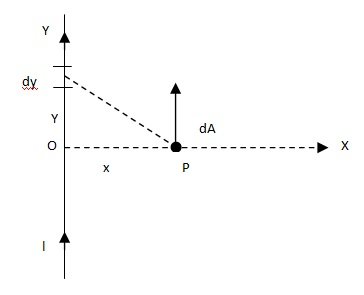
Consider a wire of length L, carrying a current I. Let P be a point at a distance x from the wire. Let O be the origin of coordinate system, with y-axis along the current and x-axis towards the field point P. Let dy be a small element at a distance y from O. Let j be unit vector along y-axis.

The magnetic potential at P due to the element dy is
    dA = μ₀I/4π dy/r directed along the current.
        = μ₀I/4π dy/√(x² + y²) j                                … (1)

The magnetic potential at P due to the whole wire is
    A = j μ₀I/4π ʃ dy/√(x² + y²)
        = j μ₀I/4π [log {y + √(x² + y²)}] +L/2
        = j μ₀I/4π log {L/2 + √(L2/4 + x²) / - L/2 + √(L2/4 + x²)}
        = j μ₀I/4π log [L/2{1 + (1 + 4x²/L²)1/2} / L/2 {-1 + (1 + 4x²/L²)1/2}]            … (2)

If the wire is infinitely long, then x2/L2 << 1. Hence Eq. (2) reduces to
    A = j μ₀I/4π log [1 + (1 + 4x²/L2) } / -1 + (1 + 4x²/L2)]
    = j μ₀I/4π log [(2 + 2x²/L2) / (2x²/L2)]
    = j μ₀I/4π log (1 + L2/x²)
    = j μ₀I/4π log (L/x) 2                     (. : L²/x² >> 1)
. :    A = (μ₀/4π) 2I log (L/x) j                                    … (3)
This is required expression for A.
. :     B = ∇ x A = ∇ x (μ0/4π 2l log (log (L/x) j)
    = μ₀/4π 2I ∂/∂x [log (l/x)] k
. :    B = μ₀/4π (2I/x) k

The magnetic field has magnitude μ₀/4π (2l/x) and is directed perpendicular to plane of paper downwards.