Monochromatic Plane Waves Travelling in an Arbitrary Direction

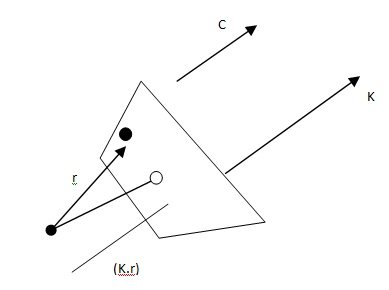
Let K be the propagation (wave) vector pointing in the direction of propagation. The magnitude of k is the wave number k. Then, (k.r) is the generalization of kx.

Considering the vector nature of the electromagnetic field, we express the spatial and temporal dependence of field vectors as
        E(r, t) = E₀ ei(k.r – ωt)n                            … (1)
        B(r,t) = 1/c E₀ ei(k.r – ωt) (k x n) = 1/c k x E                    … (2)

Here, n is the polarization vector. The actual (real) electric and magnetic fields in a monochromatic plane wave with propagation vector K and polarization n are

        E(r.t) = 1/c E₀ cos(k.r – ωt)n                        … (3)
        B(r.t) = 1/c E₀ cos(k.r – ωt)(k x n)                        … (4)



For more help in Monochromatic Plane Waves Travelling in an Arbitrary Direction please click the button below to submit your homework assignment.