Monochromatic Plane Waves in Vacuum

The electric and magnetic field vectors E and B in empty space, satisfy the three-dimensional wave equation
        ∇² E = 1/c² ∂²E/∂t², ∇²B = 1/c² ∂²B/∂t²                     … (1)
Here, c = 1/√ϵ₀μ₀ is the speed of light in vacuum.

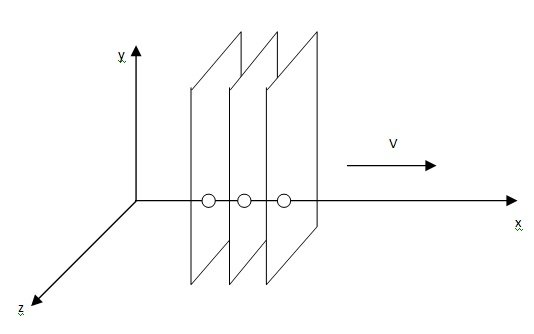
We consider sinusoidal waves of frequency ω. Such waves are called monochromatic. Suppose the waves are travelling in the x-direction and have no y – or z-dependence These are called plane waves, because the fields are uniform over every plane perpendicular to the direction of propagation.

    E(x,t) = E₀ e^{i(kx – ωt)}, B(x,t) = B₀e^{i(kx – ωt)}                    … (2)
K is called the wave number.

E₀ and B₀ are the complex amplitudes of the electric and magnetic fields. The physical fields are the real parts of E and B.

Since ∇.E = 0 and ∇.B = 0, it follows that
        (E₀)x  = (B₀)x = 0
This implies that electromagnetic waves are transverse.
The electric and magnetic fields are perpendicular to the direction of propagation.

Faraday’s law, ∇ x E = - ∂B/∂t, implies a relation between the electric and magnetic amplitudes.
-    K(E₀)_z = ω(B₀)_y         k(E₀)_y = ω(B₀)_z
Or    B₀ = k (I x E₀)/ω

E and B are in phase and mutually perpendicular. The real amplitudes of E and B are related by
            B₀ = k E₀/ω = 1/c E₀

For more help in Monochromatic Plane Waves in Vacuum please click the button below to submit your homework assignment.