Nodal Analysis With Current Sources

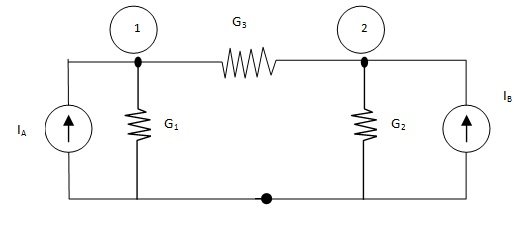
A node is defined as a junction of two or more branches. If we now define one node of any network as a reference (that is, a point of zero potential or ground), the remaining nodes of the network will all have a fixed potential relative to this reference. For a network of N nodes, therefore, there will be exist (N-1) nodes with a fixed potential relative to the assigned reference node. Equations relating these nodal voltages can be written be applying Kirchhoff’s current law at each of the (N – 1) nodes. To obtain the complete solution of a network, the resulting equations are solved for nodal voltages.

Circuits which has two nodes, 1 and 2, in addition to the reference node 0. It has known current sources IA and IB and known conductance G₁, G₂ and G₃. We need to find the voltage V₁ at node 1 and the voltageV2 at node 2, both with reference to the common node 0. Then, we may find all the branch currents by simply applying Ohm’s law. Summing the currents at node 1,
        I_A = V₁G₁ + (V₁ – V₂) G₃                                 … (1)

Summing the currents at node 2,
        I_B = V₂ G₂ – (V₁ – V₂) G₃                                 … (2)

These equations may be rearranged as follows:
        I_A = (G₁ + G₃) V₁ – G₃V₂                                … (3)
        I_B = -G₃ V₁ + (G₂ + G₃) V₂                             … (4)

These are two simultaneous algebraic equations in the two variables V₁ and V₂.
Solving these equations, V₁ and V₂ are determined.



For more help in Nodal Analysis With Current Sources click the button below to submit your homework assignment.