Potential at any Point due to a Magnetic Shell

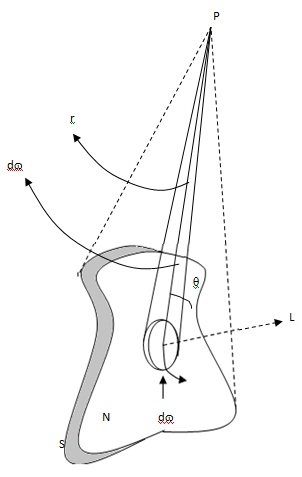
Consider a uniform magnetic shell of strength Φ. Let P be a point at a distance r from the centre O of a shell. Let OP make an angle θ with the normal to the shell, i.e., with the direction of magnetization OL. To find the potential at the point P, the sell, may be imagined to be divided into a large number of elementary area. Consider a small element of area dA of the shell around O.
The magnetic moment of the element, m = Φ dA, directed along OL.
. : Magnetic moment of the element along OP = Φ dA cos θ
Potential at P due to the element of area dA is
    dV = μ₀/4π ΦdA cos θ/r²
But dA cos θ/r² = dω, the solid angle subtended by the element at P.
. : dV = μ₀/4π Φ dω
The potential due to the whole shell is the sum of the potential due to all such elements.
The total potential at P due to the entire shell is given by
    V = μ₀/4π ∫ Φ dω
For a uniform magnetic shell, Φ is the same at all points.
. :    V = μ₀/4π Φ ∫dω
Or    V = μ₀/4π Φω    (In Vacuum)
Where ω is the solid angle subtended at P by the entire shell.
Thus the magnetic potential at a point due to a uniform magnetic shell is μ₀/4π times the produce of the strength of the shell and the solid angle subtended by the shell at the point.
(i)    If the point P lies on the side of the face having north polarity the potential at P is considered positive.
(ii)    If the point P lies on the side of the face having south polarity the potential at P is negative.

Special Cases

1.    Potential inside and outside a closed spherical shell

(i)    If the point is outside the shell, ω = 0            . :    v = 0
(ii)    If the point is inside the shell, ω = 4π            . :    v = μ₀Φ
The strength of the magnetic shell Φ is the same at all points of the shell. Hence V is uniform inside the shell. Therefore, the magnetic field inside the shell is zero.

2.    Infinitely long plane shell

Consider an infinitely long plane magnetic shell. If the point P1 lies on the side of N-pole, then potential at P1 is
        V = μ₀/4πΦω = μ₀/4πΦ .2π
Similarly, if the point P2 is on the face having south polarity.
        V = - μ₀Φ/2
. : Magnetic potential difference between two points exactly opposite to each other, once on each face of the shell
        = μ₀Φ/2 – (–μ₀Φ/2) = μ₀Φ

For more help in Potential at any Point due to a Magnetic Shell please click the button below to submit your homework assignment.