Potential at a Point on the Rim of the Disc

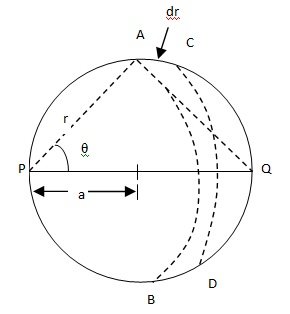
Now we shall calculate the potential at a point P lying on the edge of the disc.  Now we divide the disc into a large number of rings with P as the centre. Let us consider a ring with P as centre, r as radius and dr the thickness.

The length of the segment is 2r θ.
The area is 2r θ dr.
The charge on this segment is
    dq = 2r θ dr
Potential at P due to this segment
    dV = 1/4πε₀ dq/r = 1/4π ε₀ 2rθ dr σ/r     

The potential V at P due to the whole disc is
    V = ∫ 1/4π ε₀ . 2rθ dr σ/r = σ /2π ε₀ ∫ θ dr
From right angled triangle PAQ,
R = 2a cos θ                    . : dr = - 2a sin θ d θ.

Now When r = 0, cos θ = 0, hence θ = π/2
and    where r = 2a, cos θ = 0, hence θ =0.
    . :     V = σ/2πε₀ ∫ = -2a θ sin θ dθ = σa/π ε₀ ∫ θ sin θ dθ
        = σ/πε0 [sin θ – θ cos θ]^π/2
    . :    V = σa/πε₀


For more help in Potential at a Point on the Rim of the Disc click the button below to submit your homework assignment.