The Divergence of B

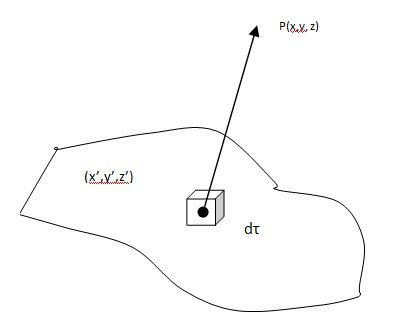
The Biot-Savart law for volume current is
        B = μ₀ /4π ∫ J x r/r₂ dτ                                … (1)

This formula gives the magnetic field at a point P = (x, y, z) in terms of an integral over the current distribution J (x’ y’ z’).
Here,
    B is a function of (x, y, z)
    J is a function of (x’, y’, z’)
    r = (x – x’)I + (y – y’)j + (z – z’)k
    dτ = dx’ dy’ dz’
The integration is over the primed coordinates (x’, y’, z’).
The divergence is to be taken with respect to the unprimed coordinates (x, y, z).
Taking divergence of both sides of Eq. (1),
    ∇.B = μ₀/4π ∫ ∇. (J x r/r²)dτ                                … (2)

But ∇ x J = 0, because J doesn’t depend on the unprimed variables (x, y, z).
    Also, ∇ x (r/r₂) = 0.
Thus the R.H.S. of Eq. (3) is zero. Hence the R.H.S. of Eq. (2) is zero.
. :         ∇.B = 0.

i.e, The magnetic field is solenoidal.
   

For more help in The Divergence of B click the button below to submit your homework assignment