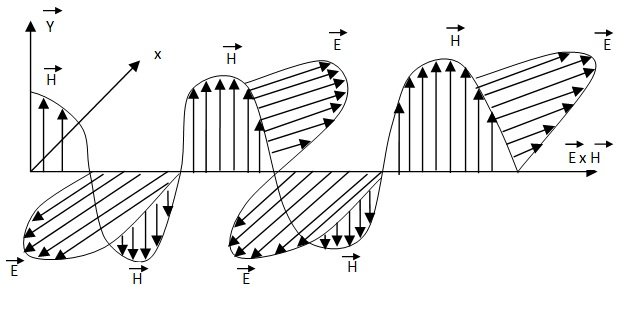
Transverse Nature of Electromagnetic Waves

Consider an electromagnetic wave propagating in free space along z-direction. E and H will vary only in the direction of z-axis, i.e.,
        ∂/∂x = ∂/∂y = 0 and ∂/∂z ≠ 0.
Such a wave is said to be plane wave. Since its vectors are function of (z, t) only, we write
        E = E (z, t)}
        H = H (z, t)}                                    … (1)
Maxwell’s first equation gives:
        ∇. D = 0, or ε₀ (∇.E) = 0
Or        ∇. E = 0, or ∂Ez /∂z = 0
. :        Ez constant in space

Similarly second equation gives
        ∇. B = 0, or μ₀ (∇.H) = 0
Or        ∇. H = 0, or ∂Hz /∂z = 0
. :        Hz = constant in space
Using third equation,
        ∇ x E = - ∂B/∂t
Or        (∇ x E)z = - μ₀ ∂Hz /∂t
Or    k(∂Ey/∂x - ∂Ex/∂y) = - μ₀ ∂Hz/∂t
Or        ∂Hz /∂t = 0
    Hz = constant in time
Similarly, by using fourth equation it can be shown that
    Ez = constant in time

Thus we arrive at the conclusion that Es and Hz are constant as regards to time and space. Thus they represent static components and consequently, no part of wave motion. We can, therefore, write
            Ez = Hz = 0
So that
            E = iEx + j Ey}
            H = IHx + j Hy}                                … (2)

Since the electric vector E and the magnetic vector H do not have any z component, the z-direction being the direction of propagation, both these vectors are perpendicular to the direction of propagation. Maxwell’s electromagnetic waves are, therefore, purely transverse.



For more help in Transverse Nature of Electromagnetic Waves click the button below to submit your homework assignment.