Uses of Operator j in Study of A.C. Circuits

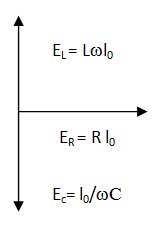
The operator j is defined as a quantity which is numerically equal to √ (-1) and which represents the rotation of a vector through 90 degree in anti clockwise direction. The above facts about j are helpful in studying the A.C. circuits. We know that in A.C. circuits, E_L and E_C always lie at 90 in anticlockwise and clockwise direction respectively with respect to ER. Hence total emf of a circuit having L, C, R will be
        E = E_R + jE_L – jE_C

Ordinarily a source of alternating e.m.f. E is denoted by E0 sin ωt.
This is actually the imaginary part of the complex form of alternating e.m.f.,
        E = E₀e^jωt
The instantaneous current in the A.C. circuit has been expressed as I = I₀ sin (ωt – Φ). This expression is the imaginary part of the complex current given by
        I = I₀e^{j(ωt – Φ)}
Since the voltage across the inductor leads the current passing through it by 90 degree, the inductive reactance ωL can be written as jωL Z_L = jω_L = jX_L.

Since the voltage across the capacitor lags the current passing through it by 90 degree, the capacitive reactance 1/ωC can be written as –j/ωC = 1/jωC. Z_C = 1/jωC = – j/ωC = - jXC.

A complex impedance can be written as the sum of a real term and imaginary term which are to be called resistance and complex reactance respectively,
        Z = R + jX
    Where X = X_L - X_C is the effective reactance in the circuit.