Node Voltage Theorem
Node Voltage Theorem Assignment Help | Node Voltage Theorem Homework Help
Node Voltage Theorem
Any junction o, two or more branches of a network is called a node. For application of node voltage theorem one of the nodes is taken as reference node or zero-potential node or datum node and the p.d. between each of the other nodes and the reference node is expressed in terms of an unknown voltage (symbolized as V1, V2 or VA, Va or Vx Vy etc.) Like Maxwell circulating current theorem node-voltage theorem reduces the number of equations to be solved to determine the unknown quantities. We shall now look at an example in which two unknown voltages VA and Va will be evaluated and then unknown currents will be determined.
Q. Find the currents in various branches of the network given below.
Solution : Let the node C be taken as reference node and the potentials of nodes A and B with reference to node C be VA and Va volts respectively Let the current direction be, as shown on the circuit diagram arbitrarily.
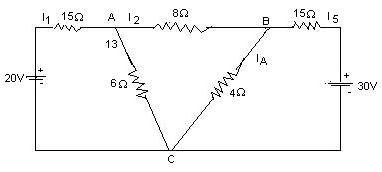
From circuit diagram for node A
I1 = 20-VA
15
I2 = VA-VB
8
I2 = VA
6
Similarly for node B
I4 = VB
4
I5 = 30-VB
15
Now applying Kirchhoff’s first law to nodes A and B we get
I1 = I2 + I3
20-VA = VA -VB + VA
8 6
and I4 = I2+ I5
or VB = VA-VB + 30-VB
4 8 15
Multiplying expressions (vi) and (vii) by 120 and rearranging the terms we get
43 VA-15B =160
53 VB-15 VA =240
Solving expressions (viii) and (ix) we get
VA = 6,040 voltage and VB = 6,360 V
1,027 1,027
Substituting values of VA and Vn in expressions (i), (ii), (iii) (iv) and (v) we get
20 - 6040
Current supplied by 20-V battery, I1 = 1027 = 0.9412 A
15
6040 - 6320
Current through 8 Ω resistor, I2 = VA - VB = 1027 1027 = - 0.0389 A
8 8
i.e. Current of 0.0389 A flowing from B to A
Current through 6- Ω resistor, I3= VA = 6040 = 0.98 A
6 6X1027
Current through 4- Ω resistor, I4 = VB = 6360 =1.5482 A
4 4X1027
30- 6360
Current supplied by 30-V resistor,I5 = 30-VB = 1027 = 1.5871A
15
For more help in Node Voltage Theorem click the button below to submit your homework assignment
Q. Find the currents in various branches of the network given below.
Solution : Let the node C be taken as reference node and the potentials of nodes A and B with reference to node C be VA and Va volts respectively Let the current direction be, as shown on the circuit diagram arbitrarily.
From circuit diagram for node A
I1 = 20-VA
15
I2 = VA-VB
8
I2 = VA
6
Similarly for node B
I4 = VB
4
I5 = 30-VB
15
Now applying Kirchhoff’s first law to nodes A and B we get
I1 = I2 + I3
20-VA = VA -VB + VA
8 6
and I4 = I2+ I5
or VB = VA-VB + 30-VB
4 8 15
Multiplying expressions (vi) and (vii) by 120 and rearranging the terms we get
43 VA-15B =160
53 VB-15 VA =240
Solving expressions (viii) and (ix) we get
VA = 6,040 voltage and VB = 6,360 V
1,027 1,027
Substituting values of VA and Vn in expressions (i), (ii), (iii) (iv) and (v) we get
20 - 6040
Current supplied by 20-V battery, I1 = 1027 = 0.9412 A
15
6040 - 6320
Current through 8 Ω resistor, I2 = VA - VB = 1027 1027 = - 0.0389 A
8 8
i.e. Current of 0.0389 A flowing from B to A
Current through 6- Ω resistor, I3= VA = 6040 = 0.98 A
6 6X1027
Current through 4- Ω resistor, I4 = VB = 6360 =1.5482 A
4 4X1027
30- 6360
Current supplied by 30-V resistor,I5 = 30-VB = 1027 = 1.5871A
15
For more help in Node Voltage Theorem click the button below to submit your homework assignment