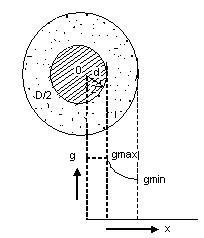
Since cable is a from ef cylindrical condenser, therefore electric intensity at a distance x from the centre O of the cable is given by (as calculated in foregoing Art)

Ex =     q     .  1 V/m
       2π∈o∈r  x

Since potential gradient = Electric intensity

 g =   q       .  1 V /m
     2π∈_o∈_r    x

From Art.

 V =    q        loge D
      2π∈_o∈_r        d
 
or  q = 2π∈_o∈_rV
          loge D
                 d

Substituting the value of q from in equation (i) we get

g = 2π∈_o∈_rV  .     1         . 1 V/m
       loge D        2π∈_o∈_r   x
              d

  =    V       
    x loge D      volts/metre
             d
Since potential gradient obvious from expression, therefore potential gradient will be maximum when x is minimum i.e. x = d and potential gradient will be minimum when x is maximum i.e. x = D
                         2                                                                                                   2
Maximum and minimum values of potential gradient are given by

gmax =     2V       volts/metres and gmin =      2V          volts/metre.
            d loge D                                          D loge D
                      d                                                    d

For more help in Potential Gradient In The Cable click the button below to submit your homework assignment