Circulation
Circulation Assignment Help | Circulation Homework Help
Circulation
• In rotational motion, circulation is a very useful concept.
• Circulation around a closed curve C is defined as the line integrate of the tangential component of the velocity taken round a closed curve C, taken positive in anticlockwise direction. The flow along a closed curve called as circulation.
• E.g flow in eddies and vortices.
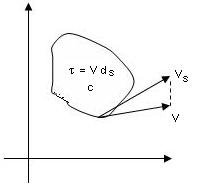
• The limiting value of circulation divided by the area fo the closed contour is called as vorticity.
Γ / Area enclosed by curve C = 2 X rotation perpendicular to area.
• The quantity 2 ω is known as vortices which is a vector quantity. Vortices is denoted by .
ζz = 2ωz
• Circulation around a closed curve C is defined as the line integrate of the tangential component of the velocity taken round a closed curve C, taken positive in anticlockwise direction. The flow along a closed curve called as circulation.
• E.g flow in eddies and vortices.
Circulation Concept
• The limiting value of circulation divided by the area fo the closed contour is called as vorticity.
Γ / Area enclosed by curve C = 2 X rotation perpendicular to area.
• The quantity 2 ω is known as vortices which is a vector quantity. Vortices is denoted by .
ζz = 2ωz
(a) Circulation around curve (b) Circulation around elementary
The circulation around an elementary rectangle with sides parallel to the axes X and Y as shown in.
Circulation along AB = ( u - ∂u / ∂y . ∂y / 2) δx
Circulation along BC = ( v + ∂v / ∂x . ∂x / 2) ∂y
Circulation along CD = - ( u - ∂u / ∂y . ∂y / 2) δx
Circulation along DA = - ( v - ∂v / ∂x . ∂x / 2) δy
For more help in Circulation click the button below to submit your homework assignment