Compressibility
Compressibility Assignment Help | Compressibility Homework Help
Compressibility
• It is the measure of elasticity in fluid.
• Fluids are compressed under pressure due to change in their mass density
• More mass can be accommodated in the unit volume and when pressure is removed the fluids regains to its original volume.
• As the pressure is increased, the volume is decreased.
dp ∝- dv / V
dp = K x -dv / V
K = dp / (-dV / V)
Where K is the constant of proportionality is known as bulk modulus.
• If K is more, dv/v is less indicating less volume change i.e. less compressibility. That is why compressibility expressed as inverse of bulk modulus.
• Higher the bulk modulus less is the compressibility of fluid
• Liquids are generally considered to be incompressible. For instance, a pressure of 113078 kPa will cause a given volume of water to decrease by only 5% from its volume at atmospheric pressure.
• Gases on the other hand, are very compressible. The volume of a gas can be readily changed by exerting an external pressure on the gas.
• Water hammer and cavitations are the examples of the importance of compressibility effects in liquid flows.
• Compressibility effects are very important in the design of modern high-speed aircrafy, missile power plants, fans and compressors
• Fluids are compressed under pressure due to change in their mass density
• More mass can be accommodated in the unit volume and when pressure is removed the fluids regains to its original volume.
• As the pressure is increased, the volume is decreased.
dp ∝- dv / V
dp = K x -dv / V
K = dp / (-dV / V)
Where K is the constant of proportionality is known as bulk modulus.
• If K is more, dv/v is less indicating less volume change i.e. less compressibility. That is why compressibility expressed as inverse of bulk modulus.
• Higher the bulk modulus less is the compressibility of fluid
• Liquids are generally considered to be incompressible. For instance, a pressure of 113078 kPa will cause a given volume of water to decrease by only 5% from its volume at atmospheric pressure.
• Gases on the other hand, are very compressible. The volume of a gas can be readily changed by exerting an external pressure on the gas.
• Water hammer and cavitations are the examples of the importance of compressibility effects in liquid flows.
• Compressibility effects are very important in the design of modern high-speed aircrafy, missile power plants, fans and compressors
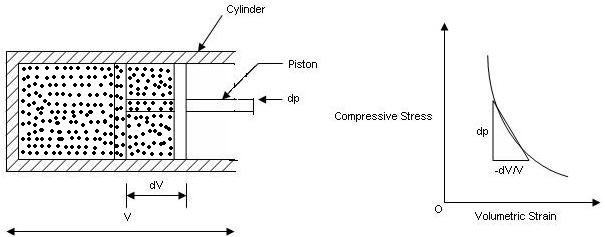
Bulk Modulus:
• It is the ratio of compressive stress to volumetric strain. It si denoted by ‘K’.
K = Increased in pressure / Volumetric strain
K = dp / -(dV / V)
V = Volume of gas enclosed in cylinder
dv = Change in volume
dp = Change in pressure
• Negative sign indicates decrease in volume with an increase in pressure.
• Value of K; Water is 2.05 x 109 N/m2 , Air is 1.02 x 105 N/m2
For more help in Compressibility click the button below to submit your homework assignment
K = Increased in pressure / Volumetric strain
K = dp / -(dV / V)
V = Volume of gas enclosed in cylinder
dv = Change in volume
dp = Change in pressure
• Negative sign indicates decrease in volume with an increase in pressure.
• Value of K; Water is 2.05 x 109 N/m2 , Air is 1.02 x 105 N/m2
For more help in Compressibility click the button below to submit your homework assignment