Continuity equation is based on the principle of conservation of mass. It states, “When a fluid flowing though the pipe at any section, the quantity of fluid per second remains constant”.


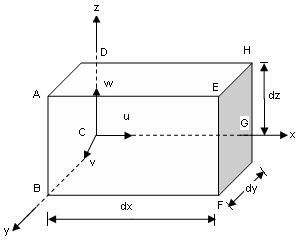
Consider a fluid element of lengths dx, dy, dz in the direction of x, y, z.

Let u, v, w are the inlet velocity components in x,y,z direction respectively.

Let  ρ is mass density of fluid element at particular instate.
Mass of fluid entering the face ABCD (In flow)
 
                                                        = Mass density x Velocity x-direction x area of ABCD

= ρ x u x (∂y x ∂z)

Then mass of fluid leaving the face EFGH (out flow)  = (ρu∂y . ∂z) + ∂ / ∂x (ρu∂y∂z)

Rate of increases in mass x-direction = Outflow – Inflow

= [ (ρudydx) + ∂ / ∂_x (ρudydz) d_x ] - (ρudydz)

Rate of increases in mass x direction  = ∂ / ∂_x  ρ u d_x d_y d_z

Similarly,

Rate of increase in mass y-direction = ∂ / ∂y ρ v ∂x ∂y ∂z

Rate of increases in mass z-direction = ∂ / ∂_z  ρ w ∂_x ∂y ∂_z

Total rate of increases in mass = (7.7.3) + (7.7.4) + (7.7.5)

=  ∂_x ∂_y ∂_z [ ∂ρu / ∂_x + ∂ρv / ∂_y + ∂ρw / ∂_z ]

By law of conservation of mass, there is no accumulation of mass, and hence the above quantity must be zero.

∂x . ∂y. ∂z [ ∂ρu / ∂_x + ∂ρv / ∂_y + ∂ρw / ∂_z ] = 0

∂ (ρu) / ∂_x +∂ (ρv) / ∂_y + ∂ (ρw) / ∂_z = 0........for compressible fluid

If fluid is incompressible, then is constant

∂_u / ∂_x + ∂_v / ∂_y + ∂_w / ∂_z = 0

This is the continuity equation for three-dimensional flow.

NOW, for tow-dimensional flow, the velocity component w = 0

Hence continuity equation is,  ∂_u / ∂_x + ∂_v / ∂_y  = 0

For more help in Continuity Equation in Three-dimensions click the button below to submit your homework assignment