Continuity Equation in a Polar Form
Continuity Equation in a Polar Form Assignment Help | Continuity Equation in a Polar Form Homework Help
Continuity Equation in a Polar Form
Consider a two-dimensional incompressible flow field. The two dimensional polar coordinates are ‘r’ and θ angle subtended by elements is 'dθ' . Consider a fluid elements ABCD between radius ‘r’ and (r + dr) dθ .
The components of velocity in radial direction Vr ad tangential direction Vθ.
Assume thickness of element perpendicular to the plane of paper is unity.
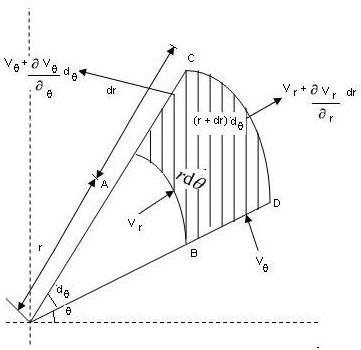
Consider flow in radial direction:
Mass if fluid entering the face AB during the time dt,
Fluid influx = Density x Velocity in r-direction x Area x Time
ρ . Vr (rdθ x 1) dt Thickness = 1
Mass fo fluid leaving the face CD during the same time dt is,
Fluid efflux = ρ ( Vr + ∂ vr / ∂r dr ) (r + dr) dθ . dt
Mass accumulated in element = Fluid influs-Fluid efflux
ρVr . rdθ . dt - [ ∂vr rdθdt + ρ ∂vr / ∂r . r. drdθ . dt + ρVr . dr . d . dt + ρ dvr / dr . d2 rdθdt ]
Neglect d2r is too small,
= - [ ρVr. dr. dθ . dt + ρ dV / dr . r. dr . dθ . dt
= - ρ [ Vr + dVr / dr ] dr . dθ .dt
= - ρ [ Vr / r + dV / dr ] rdr . dθ .dt
This is written in this form because is the volume f elemtn.
Consider flow in tangential direction,
= [Mass of fluid entering BC- Mass of fluid leaving CD] dt
= [ ρ Vθ . dr x - ρ (Vθ + ∂Vθ / ∂θ . dθ) dr ] dt
= [ ρ Vθ drdt - ρ Vθ drdt - ∂Vθ / ∂θ . dθ. drdt ]
= - ∂Vθ / ∂θ ρdθ . drdt
= - ∂ / ∂θ Vθ rdθ . drdy / r ( Multiplying and divide by r)
= - 1/r Vθ / ∂θ (rdr/ dθ / dt)
According law of conservation of mass, “The total gain mass be equal to the rate of change of luid mass in element ABCD”.
Total gain of mass = Mass accumulate due to radial + Mass accumulate due to tangential
= - [ ρVr + ρ dV / dr ] drdθ . dt + [ ρ ∂Vθ / ∂θ . dθ. dr .dt ]
But, mass of fluid element = ρ x volume of fluid element.
= ρ [ rdθ . drdt ]
Rate of increases of fluid mass in element with time,
= ∂ / ∂t [ ρ rdθ + (r+dr) d / 2 dr dt
= ∂ / ∂t ρ ( rdθ / 2 + rdθ / 2 + drdθ / 2) drdt
dr x dθ = 0
By law of conservation,
∂ / ∂t ( ρ. r. dθ. dr) dt = - [ ρVr + ρr dVr / dr. r + ρ ∂Vθ / ∂θ ] dr. dθ .dt
Consider dt = 1,
∂ / ∂t ( ρ. r. dθ. dr) + [ ρVr + r dVr / dr. r + ρ ∂Vθ / ∂θ ] dr. dθ .dt = 0
For steady flows ∂ / ∂t = 0
[ ρVr + ρ ∂ / ∂r (Vr) r + ∂ / ∂θ ] dr. dθ = 0
For incompressible flow, ρ = constant.
Vr + ∂ / ∂r (Vr) + ∂ / ∂θ . (Vθ) = 0
Or
∂ / ∂r (r. Vr) + ∂ / ∂ . Vθ = 0
Which is the equation of continuity in polar co-ordinates for two dimensional, steady incompressible flow.
For more help in Continuity Equation in a Polar Form click the button below to submit your homework assignment
θ ρ ∂
The components of velocity in radial direction Vr ad tangential direction Vθ.
Assume thickness of element perpendicular to the plane of paper is unity.
Consider flow in radial direction:
Mass if fluid entering the face AB during the time dt,
Fluid influx = Density x Velocity in r-direction x Area x Time
ρ . Vr (rdθ x 1) dt Thickness = 1
Mass fo fluid leaving the face CD during the same time dt is,
Fluid efflux = ρ ( Vr + ∂ vr / ∂r dr ) (r + dr) dθ . dt
Mass accumulated in element = Fluid influs-Fluid efflux
ρVr . rdθ . dt - [ ∂vr rdθdt + ρ ∂vr / ∂r . r. drdθ . dt + ρVr . dr . d . dt + ρ dvr / dr . d2 rdθdt ]
Neglect d2r is too small,
= - [ ρVr. dr. dθ . dt + ρ dV / dr . r. dr . dθ . dt
= - ρ [ Vr + dVr / dr ] dr . dθ .dt
= - ρ [ Vr / r + dV / dr ] rdr . dθ .dt
This is written in this form because is the volume f elemtn.
Consider flow in tangential direction,
= [Mass of fluid entering BC- Mass of fluid leaving CD] dt
= [ ρ Vθ . dr x - ρ (Vθ + ∂Vθ / ∂θ . dθ) dr ] dt
= [ ρ Vθ drdt - ρ Vθ drdt - ∂Vθ / ∂θ . dθ. drdt ]
= - ∂Vθ / ∂θ ρdθ . drdt
= - ∂ / ∂θ Vθ rdθ . drdy / r ( Multiplying and divide by r)
= - 1/r Vθ / ∂θ (rdr/ dθ / dt)
According law of conservation of mass, “The total gain mass be equal to the rate of change of luid mass in element ABCD”.
Total gain of mass = Mass accumulate due to radial + Mass accumulate due to tangential
= - [ ρVr + ρ dV / dr ] drdθ . dt + [ ρ ∂Vθ / ∂θ . dθ. dr .dt ]
But, mass of fluid element = ρ x volume of fluid element.
= ρ [ rdθ . drdt ]
Rate of increases of fluid mass in element with time,
= ∂ / ∂t [ ρ rdθ + (r+dr) d / 2 dr dt
= ∂ / ∂t ρ ( rdθ / 2 + rdθ / 2 + drdθ / 2) drdt
dr x dθ = 0
By law of conservation,
∂ / ∂t ( ρ. r. dθ. dr) dt = - [ ρVr + ρr dVr / dr. r + ρ ∂Vθ / ∂θ ] dr. dθ .dt
Consider dt = 1,
∂ / ∂t ( ρ. r. dθ. dr) + [ ρVr + r dVr / dr. r + ρ ∂Vθ / ∂θ ] dr. dθ .dt = 0
For steady flows ∂ / ∂t = 0
[ ρVr + ρ ∂ / ∂r (Vr) r + ∂ / ∂θ ] dr. dθ = 0
For incompressible flow, ρ = constant.
Vr + ∂ / ∂r (Vr) + ∂ / ∂θ . (Vθ) = 0
Or
∂ / ∂r (r. Vr) + ∂ / ∂ . Vθ = 0
Which is the equation of continuity in polar co-ordinates for two dimensional, steady incompressible flow.
For more help in Continuity Equation in a Polar Form click the button below to submit your homework assignment
θ ρ ∂