Equation Of Free Vortex Flow
Equation Of Free Vortex Flow Assignment Help | Equation Of Free Vortex Flow Homework Help
Equation of Free Vortex Flow
In case of free vortex flow
We know,
dp = ρv2 / r dr - ρg dr put v = C/r
dp = ρ x C2 / r3 dr-ρ g dz
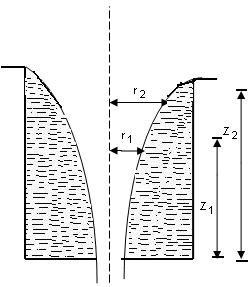
Consider two points 1 and 2 in fluid having radius r1 and r2 respectively from the central axis and their height being z1 and z2 from bottom of the vessel.
Integrating Equation for point 1 and 2.
2 2 2
∫ dp = ∫ ρ C2 / r3 dr - ∫ ρ g dz
1 1 1
2 2
p2 - p1 = ρ C2 ∫ r-3 dr - ρ g ∫ dz
1 1
= ρ C2 ( r-3+1 / -3+1)12 - ρ g (Z)12 = ρ C2 (-1 / 2r2 )12 - ρ g (z2 - z1)
= ρC2 / 2 [ 1/2 r2 1/2 r2 ] - ρ g (z2 - z1) = - ρ / 2 (v22 - v12) - ρ g (z2 - z1)
where v2 = c2 / r2 and v1 = c1 / r1
P2 - P1 = ρ/2 (v12 - v22) - ρ g ( z2 - z1)
dividing both side by ρg
P2 - P1 / ρg = v12 - v22 / 2g - ( z2 + z1)
P2 / γ - P1 / γ = V12 / 2g - v22 / 2g - z2 + z1
P1 / γ + v12 / 2g + z1 = P2 / γ + v22 / 2g + z2
Bernoulli’s equation is applicable for free vortex flow.
For more help in Equation of Free Vortex Flow click the button below to submit your homework assignment
We know,
dp = ρv2 / r dr - ρg dr put v = C/r
dp = ρ x C2 / r3 dr-ρ g dz
Consider two points 1 and 2 in fluid having radius r1 and r2 respectively from the central axis and their height being z1 and z2 from bottom of the vessel.
Integrating Equation for point 1 and 2.
2 2 2
∫ dp = ∫ ρ C2 / r3 dr - ∫ ρ g dz
1 1 1
2 2
p2 - p1 = ρ C2 ∫ r-3 dr - ρ g ∫ dz
1 1
= ρ C2 ( r-3+1 / -3+1)12 - ρ g (Z)12 = ρ C2 (-1 / 2r2 )12 - ρ g (z2 - z1)
= ρC2 / 2 [ 1/2 r2 1/2 r2 ] - ρ g (z2 - z1) = - ρ / 2 (v22 - v12) - ρ g (z2 - z1)
where v2 = c2 / r2 and v1 = c1 / r1
P2 - P1 = ρ/2 (v12 - v22) - ρ g ( z2 - z1)
dividing both side by ρg
P2 - P1 / ρg = v12 - v22 / 2g - ( z2 + z1)
P2 / γ - P1 / γ = V12 / 2g - v22 / 2g - z2 + z1
P1 / γ + v12 / 2g + z1 = P2 / γ + v22 / 2g + z2
Bernoulli’s equation is applicable for free vortex flow.
For more help in Equation of Free Vortex Flow click the button below to submit your homework assignment