Adjoint Of A Square Matrix
Adjoint Of A Square Matrix Assignment Help | Adjoint Of A Square Matrix Homework Help
Adjoint of A Square Matrix
We now return our discussion to matrices.
Definition. Let A = (aij) be a square matrix of order n and let Cij be the cofactor of aij in the determinant |A|. Then the adjoint of A, denoted by adj A, is defined as the transpose of the cofactor matrix (Cij)
Thus the adjoint of a square matrix A is obtained on replacing each (i,j)th element of A by the cofactor of the (j,i)th element in |A|.
Example. Find adj A, if
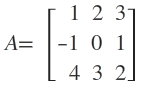
Solution. We have
C11 = -3 C12 = 6 C13 = -3
C21 = 5 C22 = -10 C23 = 5
C31 = 2 C32 = -4 C33 = 2
Thus,
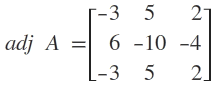
For more help in Adjoint of A Square Matrix click the button below to submit your homework assignment
Definition. Let A = (aij) be a square matrix of order n and let Cij be the cofactor of aij in the determinant |A|. Then the adjoint of A, denoted by adj A, is defined as the transpose of the cofactor matrix (Cij)
Thus the adjoint of a square matrix A is obtained on replacing each (i,j)th element of A by the cofactor of the (j,i)th element in |A|.
Example. Find adj A, if
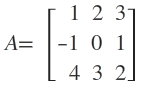
Solution. We have
C11 = -3 C12 = 6 C13 = -3
C21 = 5 C22 = -10 C23 = 5
C31 = 2 C32 = -4 C33 = 2
Thus,
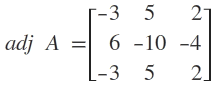
For more help in Adjoint of A Square Matrix click the button below to submit your homework assignment