Decreasing Function
Decreasing Function Assignment Help | Decreasing Function Homework Help
Decreasing Function
A function f is said to be decreasing (abbreviated) on the interval (a,b) if f (x) decreases as x increases on the interval (a,b), that is, if the graph of f is falling from left to right.
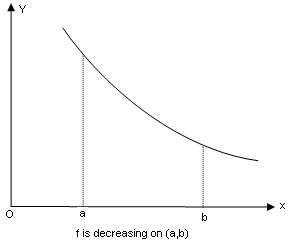
Thus f is decreasing on the interval (a,b) if we have f (x1) > (x2) whenever x1 < x2 with x1 and x2 in (a,b).
Note. The term downward sloping is also sometimes used for decreasing functions.
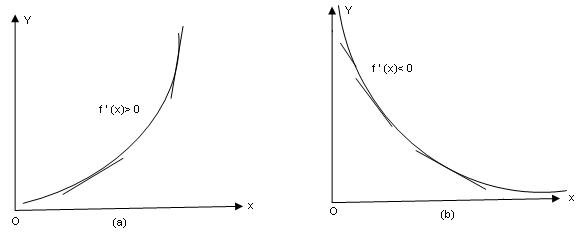
If we examine the graph of an increasing function. we see that the slope of the tangent lime at any on the curve is positive, whereas if we examine the graph of a decreasing functions, we see that the slope of the tangent line at any point on the curve is negative.
These observations together with the fact that the derivative gives the slope of the tangent line leas to the following test which allows us to use the derivative to determine when a function is increasing or decreasing.
For more help in Decreasing Function click the button below to submit your homework assignment
Thus f is decreasing on the interval (a,b) if we have f (x1) > (x2) whenever x1 < x2 with x1 and x2 in (a,b).
Note. The term downward sloping is also sometimes used for decreasing functions.
If we examine the graph of an increasing function. we see that the slope of the tangent lime at any on the curve is positive, whereas if we examine the graph of a decreasing functions, we see that the slope of the tangent line at any point on the curve is negative.
These observations together with the fact that the derivative gives the slope of the tangent line leas to the following test which allows us to use the derivative to determine when a function is increasing or decreasing.
For more help in Decreasing Function click the button below to submit your homework assignment