Product Of Tow Determinants
Product Of Tow Determinants Assignment Help | Product Of Tow Determinants Homework Help
Product of Tow Determinants
Theorem. The determinant of the product of two matrices of order n is the product of their determinants. That is, |AB| = |A| |B|.
Example. Let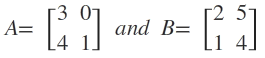
then
|AB| = |A| . |B| = = (3) (3) = 9.
= (3) (3) = 9.
Remark. Since we known that for any square matrix A, |A| = |A’|, we have |AB| = |A| |B| = |A’| |B’| = |A| |B’|. Thus, the product of two determinants can be written in terms of row by column as in matrices or unlike matrices column by column, column by row or row by row.
Example. Show that
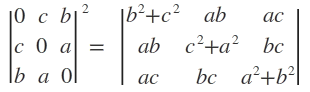
Hence evaluate the determinant on the right.
Solution. Let
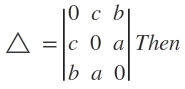
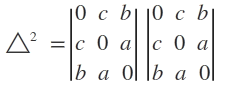
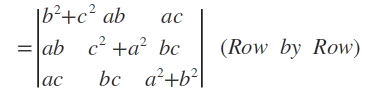
Further,
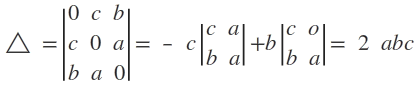
Δ2 = 4a2 b2 c2
For more help in Product of Tow Determinants click the button below to submit your homework assignment
Example. Let
then
|AB| = |A| . |B| =
Remark. Since we known that for any square matrix A, |A| = |A’|, we have |AB| = |A| |B| = |A’| |B’| = |A| |B’|. Thus, the product of two determinants can be written in terms of row by column as in matrices or unlike matrices column by column, column by row or row by row.
Example. Show that
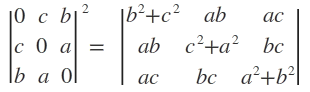
Hence evaluate the determinant on the right.
Solution. Let
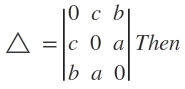
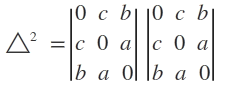
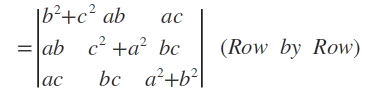
Further,
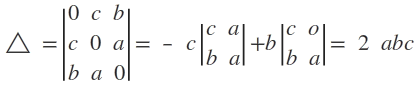
Δ2 = 4a2 b2 c2
For more help in Product of Tow Determinants click the button below to submit your homework assignment