Properties Of Determinants
Properties Of Determinants Assignment Help | Properties Of Determinants Homework Help
Properties of Determinants
We now state some useful properties of determinants of order three only. However, these properties hold for determinants of any order. These properties help a good deal in the evaluation of determinants. We use the notations Ri and Cj to denote respectively the ith row and the jth column of a determinant.
Property. The value of a determinant remains unchanged if rows are changed into columns and columns into rows. That is,
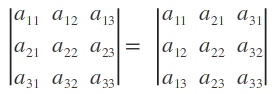
Remark. In terms of matrices, if A is square matrix, then |A| = |A’|.
Property. If any two adjacent rows (or columns) of a determinant are interchanged, the value of the determinant so obtained is the negative of the value of the original determinant. That is,
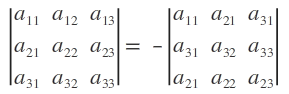
Remark. The notation Ri → k Rj (Ci → Cj) used to represent interchange of ith and jth row (column).
Property. If any two rows (or columns) of a determinant are identical, the value of the determinant is zero. That is,
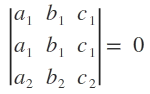
Property. If each element of a row (or column) of a determinant is multiplied by a constant by a constant k, the value of the determinant so obtained is k times the value of the original determinant. That is,
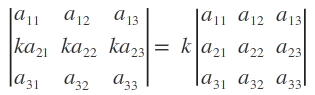
Remark. The notation Ri → k Ri (Ci → k Ci) is used to represent multiplication of each element of ith row (column) by the constant k.
Property. If to the element of a row (or column) of a determinant are added k times the elements of another row (or column), the value of the determinant so obtained is equal to the value of the original determinant. That is,
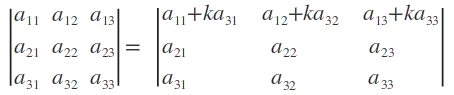
Property. If each element of a row (or column) of a determinant is the sum of two element, the determinant can be expressed as the sum of two determinant. That is,
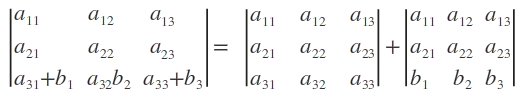
For more help in Properties of Determinants click the button below to submit your homework assignment
Property. The value of a determinant remains unchanged if rows are changed into columns and columns into rows. That is,
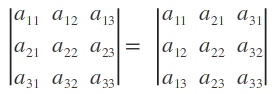
Remark. In terms of matrices, if A is square matrix, then |A| = |A’|.
Property. If any two adjacent rows (or columns) of a determinant are interchanged, the value of the determinant so obtained is the negative of the value of the original determinant. That is,
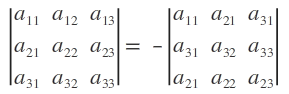
Remark. The notation Ri → k Rj (Ci → Cj) used to represent interchange of ith and jth row (column).
Property. If any two rows (or columns) of a determinant are identical, the value of the determinant is zero. That is,
Property. If each element of a row (or column) of a determinant is multiplied by a constant by a constant k, the value of the determinant so obtained is k times the value of the original determinant. That is,
Remark. The notation Ri → k Ri (Ci → k Ci) is used to represent multiplication of each element of ith row (column) by the constant k.
Property. If to the element of a row (or column) of a determinant are added k times the elements of another row (or column), the value of the determinant so obtained is equal to the value of the original determinant. That is,
Property. If each element of a row (or column) of a determinant is the sum of two element, the determinant can be expressed as the sum of two determinant. That is,
For more help in Properties of Determinants click the button below to submit your homework assignment