Rules for differentiation
Rules for differentiation Assignment Help | Rules for differentiation Homework Help
Rules for differentiation
There are rules or formulas that allow us to evaluate derivatives quickly without explicitly going through the limit process. We shall look at some rules in this section.
Rule. If c is a constant, then
d/dx (c) = 0
That is, the derivative of a constant function is zero.
Proof. Let f (x) = c. Aapplying the definition of the derivative, we obtain
f ' (x) = lim f (x+ h) - f (x)
h→0
f ' (x) = lim c-c / h = lim 0/h = 0
h→0 h→0
For example, if y = 5, then dv/dx = d 5/dx = 0
Rule. If n is any real number, then d/dx (xn) = n xn-1
That is, the derivative of a constant power of x is the exponent times x raised to a power one less than the given power.
Proof. We shall give a proof for the case when is a positive integer. Let f (x) = xn. By applying the definition of the derivative, we obtain
f ' (x) = lim f (x+ h) - f (x)
h→0 h
= lim (x + h)n - xn
h→0 h
= lim (x+h)n - xn
x+h→x (x + h) - x
= n xn-1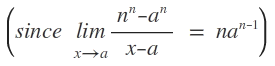
Hence f ‘ (c) = n xn-1 .
For more help in Rules for differentiation click the button below to submit your homework assignment
Rule. If c is a constant, then
d/dx (c) = 0
That is, the derivative of a constant function is zero.
Proof. Let f (x) = c. Aapplying the definition of the derivative, we obtain
f ' (x) = lim f (x+ h) - f (x)
h→0
f ' (x) = lim c-c / h = lim 0/h = 0
h→0 h→0
For example, if y = 5, then dv/dx = d 5/dx = 0
Rule. If n is any real number, then d/dx (xn) = n xn-1
That is, the derivative of a constant power of x is the exponent times x raised to a power one less than the given power.
Proof. We shall give a proof for the case when is a positive integer. Let f (x) = xn. By applying the definition of the derivative, we obtain
f ' (x) = lim f (x+ h) - f (x)
h→0 h
= lim (x + h)n - xn
h→0 h
= lim (x+h)n - xn
x+h→x (x + h) - x
= n xn-1
Hence f ‘ (c) = n xn-1 .
For more help in Rules for differentiation click the button below to submit your homework assignment