Time Reversal Test

Prof. Irving Fisher has made a careful study of the various proposals for computing index numbers and has suggested various tests to be applied to any formula to indicate whether or not it is satisfactory. The two most important of these he calls the time reversal test and the factor reversal test.

Time reversal test is a test to determine whether a given method will work both ways in time, forward and backward. In the words of Fisher, “The test is that the formula for calculating the index number should be such that it will give the same ratio between one point of comparison and the other, no matter which of the two is taken as base.” In other words, when the data for any two years are treated by the same method, but with the bases reversed, the two index numbers secured should be reciprocals of each other so that their product is unity. Symbolically, the following relation should be satisfied:

            P01 X P10 = 1

Where P01 is the index for time “I” on time “0” as base and P10 is the index for time “0” on time “I” as base. If the product is not unity, there is said to be a time bias in the method.

The test is not satisfied by Laspeyres method and the Paasche method as can be seen below:
When Laspeyres method is used



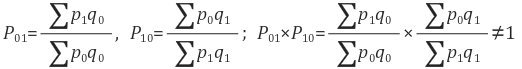
and the test is not satisfied.

When Paasche method is used


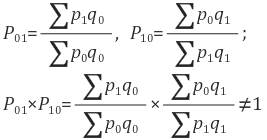
and the test is not satisfied.

There are five methods which do satisfy the test:

(1) The Fisher’s ideal formula,

(2) Simple geometric mean of price relatives,

(3) Aggregates with fixed weights,

(4) The weighted geometric mean of price relatives if we use fixed weights, and

(5) Marshall-Edgeworth method.

Let us now see how Fisher’s Ideal formula satisfies the test.

Proof:

Changing time, i.e., 0 to 1 and 1 to 0.



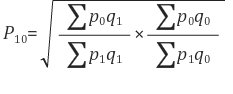
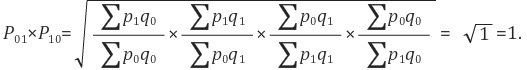
Since P01 X P10 = 1, the Fisher’s ideal index satisfies the test.

For more help in Time Reversal Test click the button below to submit your homework assignment