Non Parametric Test Sample Assignment
home > Sample Assignment > Statistics Homework Assignment > Non Parametric Test
Males : 31 25 38 33 42 40 44 26 43 35
Females: 44 30 34 47 35 32 35 47 48 34
Solutions:
Age Rank Age Rank Rank of Males
25 ___1_ 35__ 10 _______ 4
26 ___2_ 38__ 12_______ 1
30 ___3_ 40___ 13______ 12
31 ___4_ 42 ___ 14 _______ 6
32 ___ 5_ 43___ 15______ 14
33 ___ 6_ 44___ 16.5 _____ 13
34 ___7.5_ 44___ 17.5 ____ 16.5
34 ___ 7.5_ 47___ 18.5 _____ 2
35 ___10 47 ___ 18.5_____ 15
35 ___ 10 48___ 20______ 10
___________________93.5
Here n1 = 10, n2 = 10 (samples sizes need not be same)
Sum of ranks R1 = 93.5
U – statistics, U = 1112 + n1(n1 + 1) - R1
2
= 10 x 10 + 10 x 11 – 93.5
_______2
= 100 + 55 – 93.5 = 61.5
H0 = n1 + n2 observations cam from identical population U.
U = n1n2 = 10 x 10 = 50
__2_____ 2
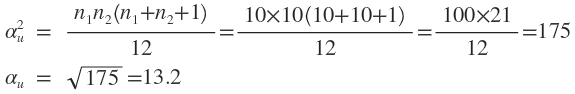
Testing the hypothesis:
H0 → μ1 ≠ μ2 i.e. there is no difference between the two populations and hence the same mean.
H1 → μ1 ≠ μ2 i.e. there is a difference between the two populations i.e., they have different means.
α = level of significance for testing H0 and H1
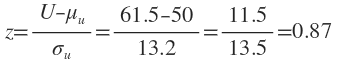
Now for a two-tailed test at 0.1 level, we would accept the hypothesis H0 if -1.64 < z > 1.64 and here z = 0.87, we conclude that the mean ages are not significantly different i.e., null hypothesis is accepted at 0.1% level.
Non Parametric Test Sample Assignment
Questions: Test the hypothesis of no difference between the ages of male and female employees of a certain company using Mann-Whitney U test for the sample data. Use the 0.10 level of significance.Males : 31 25 38 33 42 40 44 26 43 35
Females: 44 30 34 47 35 32 35 47 48 34
Solutions:
Age Rank Age Rank Rank of Males
25 ___1_ 35__ 10 _______ 4
26 ___2_ 38__ 12_______ 1
30 ___3_ 40___ 13______ 12
31 ___4_ 42 ___ 14 _______ 6
32 ___ 5_ 43___ 15______ 14
33 ___ 6_ 44___ 16.5 _____ 13
34 ___7.5_ 44___ 17.5 ____ 16.5
34 ___ 7.5_ 47___ 18.5 _____ 2
35 ___10 47 ___ 18.5_____ 15
35 ___ 10 48___ 20______ 10
___________________93.5
Here n1 = 10, n2 = 10 (samples sizes need not be same)
Sum of ranks R1 = 93.5
U – statistics, U = 1112 + n1(n1 + 1) - R1
2
= 10 x 10 + 10 x 11 – 93.5
_______2
= 100 + 55 – 93.5 = 61.5
H0 = n1 + n2 observations cam from identical population U.
U = n1n2 = 10 x 10 = 50
__2_____ 2
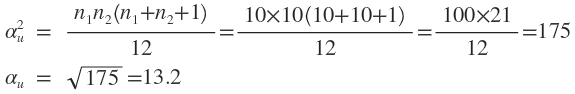
Testing the hypothesis:
H0 → μ1 ≠ μ2 i.e. there is no difference between the two populations and hence the same mean.
H1 → μ1 ≠ μ2 i.e. there is a difference between the two populations i.e., they have different means.
α = level of significance for testing H0 and H1
Now for a two-tailed test at 0.1 level, we would accept the hypothesis H0 if -1.64 < z > 1.64 and here z = 0.87, we conclude that the mean ages are not significantly different i.e., null hypothesis is accepted at 0.1% level.
Other Sample Assignments in Statistics Homework Assignment :